Логарифмы – важная тема математического анализа, которая изучается как в старшей школе, так и в курсе высшей математики. Знания по части логарифмов являются в какой-то мере фундаментальными для изучающих математику. Дальше в тексте вы найдете всю полезную информацию об изучении логарифмов на школьном этапе.
Что такое логарифмы?
Понятием «логарифм» математики пользуются с XVII века. Его изобрел и внедрил в науку шотландский ученый Дж. Напье, который находил примеры логарифмов в числовых закономерностях природы и искусства.
Логарифм являет собой математическую операцию, которая определяет, сколько раз некое число, называемое основанием, нужно умножить само на себя, чтобы получить другое число. Логарифмы связывают арифметическую и геометрическую прогрессии. Они помогают упрощать громадные вычисления и особо часто используются в навигации, геодезии, инженерии, астрономии.
Как записываются логарифмы? Возьмем показательное уравнение. Большой лист бумаги сложили в 32 слоя. В данном случае логарифм – это количество действий по складыванию бумаги, после которых имеем результат в 32 слоя. То есть основание 2, умножаемое на себя определенное количество раз, дает число 32. Сколько умножений необходимо? В математической записи это выглядит так: 
или 
Поскольку 2*2*2*2*2=32: 
Лист бумаги нужно сложить пополам 5 раз, чтобы получить 32 слоя.
До появления механических и электронных калькуляторов логарифмы считались быстрым методом вычислений. Ведь они отображают интенсивность звуков, твердость минералов и плотность кислот, расстояние между небесными телами, частотность землетрясений и прочее.
Читайте также: Интерактивная онлайн доска - ресурс, который поможет при организации онлайн урока
Свойства логарифма
Свойства логарифмов связаны с упрощением логарифмических выражений. Они очень похожи на свойства экспонент и свойства показателей степени. Рассмотрим подробнее 7 основных особенностей логарифмов:
- Если число, логарифм которого нужно определить, равно основанию логарифма, то в итоге логарифм равен 1:
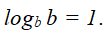
- Логарифм единицы независимо от основания равен нулю:
- Если число, логарифм которого нужно найти, равно основанию логарифма и имеет степень х, то значение логарифма будет равно числу степени:
- Логарифм произведения являет собой сумму логарифмов каждого из умножителей. Здесь, как и с показателями степени, чтобы умножить два числа с одинаковым основанием, нужно складывать экспоненты. При этом количество умножителей не имеет значения.
- Свойство логарифма частного также очень похоже на свойство показателей степени. Чтобы найти логарифм частного, нужно найти разницу между логарифмами делимого и делителя. Это выглядит так:
- Особенности логарифма степени немного отличаются от показателя степени. В случае с логарифмом степень становится умножителем.
- Если основание логарифма определенного числа имеет степень, то она становится знаменателем дроби, в которой числителем выступает единица. В итоге эту дробь нужно умножить на значение логарифма числа при условии, что степень не равна нулю. Это выглядит так:
Формулы логарифма
Математические особенности логарифмов описываются с помощью формул:
Ниже представлено, как эти формулы можно применить для преобразования логарифмических выражений и нахождения их значения. Для быстрых вычислений подойдет калькулятор логарифмов онлайн.
В профессиональном отношении логарифмы нужны для проведения банковских и различных финансовых вычислений, прогнозирования природных и демографических явлений, определения производственных затрат, проведения лабораторных измерений, физических, химических и астрономических исследований. Хорошо, если бы в школе ребенок получил крепкий математический фундамент.
Однако всегда можно обратиться к опытному репетитору, который адаптирует учебный материал под вашу цель обучения. Такого педагога можно легко найти на сайте BUKI. Вы можете сразу выбрать проверенного и квалифицированного преподавателя.
Читайте также: Лучшие университеты Центральной Азии
Уравнения с логарифмами
Главный способ решения уравнений – применение определения логарифма.
Пример 1
Пример 2
Пример 3
